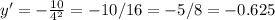Question

Can someone help me for this question?​

Answer 1

Explanation:

To find the equation of the tangent to the given function, you must differentiate the function with respect to 'x'. The derivative (y prime) will give the tangent line at any point along the function. After we find the tangent equation, we let x equal zero which will alow us to find the slope at that point.

Begin by bringing the entire denominator to the top. If not, you'll have to do the quotient rule which is very annoying 99% of the time. You will get:

`y=5(e^(2x) +3)^(-1)`

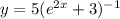
With this now, you can use the chain rule twice. Begin by differentiating:

`(dy)/(dx) =5(d)/(dx) [e^(2x) +3)^(-1)]`

Use the chain rule:

`(dy)/(dx) =-5(e^(2x) +3)^(-2)(d)/(dx) [e^(2x) +3]`

Use the chain rule again:

`(dy)/(dx) =-5(e^(2x) +3)^(-2)[2e^(2x) ]`

Simplify:

`y'=-(10e^(2x) )/((e^(2x)+3)^(2))`

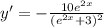
Let x = 0 to get:

`y'=-(10)/(4^(2)) =-10/16=-5/8=-0.625`