Question

Production of pressure vessels is fastening an open-ended cylinder and two rigid plates with bolts. The cylinder made of brass. The plates are attached with four W 7/16" steel bolts and nuts. These bolts have 16 threads per inch. An additional half turn is given to each of the nuts after they snugged. Calculate the pressure that the container will start to leak. Does the cylinder or bolt fail under this pressure? Take D= 16", L=16" and t= 0.125"

Answer 1

475.14 psi

Step-by-step explanation:

Given:-

- The steel bolts standard used = W 7/16''

- The number of bolts for the flange , n = 4

- The pitch of each bolt, k = 1 / 16 inch / turns

- The diameter of flange end-plate, D = 16''

- The length of useful length of bolt, L_b = 16''

- The thickness of vessel's walls , t = 0.125''

- The additional amount of turn after snug fit, T = 1/2

Find:-

Production of pressure vessels is fastening an open-ended cylinder and two rigid plates with bolts. Calculate the pressure that the container will start to leak.

Solution:-

- The end-plates ( Flanges ) experience a constant force ( F ) due to pressure "p" of the pressurized gas in the vessel.

- The force experienced due to pressure "p" by each of the end-plates can be determined from the following relation:

`F = p*A_p_l_a_t_e`

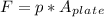
Where,

`A_p_l_a_t_e = (\pi*D^2 )/(4)`

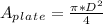
Hence,

`F = p*(\pi*D^2 )/(4)`

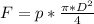
- Each end plate is fitted with n = 4 identical bolts ( W 7/16'' ). The tensile force experienced by each bolt ( Fb ) fastened into the end-plate is:

`F_b = F / n\\\\F_b = p*(\pi*D^2 )/(16)`

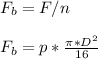
- The amount of stretch ( deformation ) in each bolt ( δb ) can be represented by Young's modulus ( E ) expression for the bolts.

`E_b = (stress)/(strain) \\\\E_b = (F_b / A_b)/(delta(b)/L_b) \\\\delta(b) = (F_b*L_b)/(A_b*E_b)`

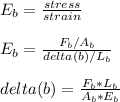
Where,

δb = delta ( b ) : The deformation in each bolt ( stretch )

E_b = Elastic modulus ( steel ) - (ASTM A-36) = 30 Mpsi

d_b = Diameter of bolt used = 5 / 8 '' ( W 7 / 16'' )

A_b =
`(\pi*d_b^2 )/(4)`

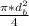
- Care must be taken when visualizing the strains in the end caps as it is subjected to poisson contraction.

- The increase in pressure "p" will induce hoop stress and consequently hoop strain. ( Radial expansion )

- According to material law, an expansion in one dimension leads to a contraction in the other dimension such that the volume of material ( pressure vessel ) used remains constant.

- Therefore, we expect to see a "poisson contraction" of the axial length of the pressure vessel.

- This advertently leads to a small clearance " c " between the end plates and the ends of the pressure vessel circumferential thickness. This very clearance becomes a source of leakage from flanged ends of the pressure vessels.

- We need to determine the minimum clearance " c " required for the leakage to occur.

- The flange bolts are tightened with "T" turns after snug fitting. These turns made chiefly using a wrench provides the requisite axial preloading of the flange end-plates against pressure vessel ends.

- The axial length through which the bolts are turned are identical for all bolts. They are mathematically expressed as:

Turned length = T*k

- For the leakage to occur the amount of axial contraction must be at-least the amount of clearance i.e turned length. Hence, the clearance is:

c = Turned length = T*k

- The axial contraction ( longitudinal deformation ) of the pressure vessel ( δc ) is simply the product of strain in the axial direction ( εa ) and length of the bolt ( L_b )

`delta ( c ) = strain ( a )*L_b`

Where,

delta ( c ) = δc ... longitudinal deformation

strain ( a ) = εa ... longitudinal strain.

- Use the appropriate stress-strain relationship for longitudinal strain ( εa ) considering the poisson ratio ( ν ).

εa =
`strain ( a ) = ( stress ( a ) - v*stress ( h ) )/(E_c)`

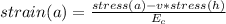
Where,

stress ( a ) = longitudinal stress = 0

( Leakage: the stress in axial direction has vanished )

stress ( h ) = Hoop stress

E_c : Modulus of elasticity of pressure vessel ( Brass )

E_c = 16.3 Mpsi , ν = 0.344

- The hoop stresses are defined as:

σh =
`stress ( h ) = (p*D)/(2*t)`

- The strain in axial direction ( εa ) would be:

εa =
`strain ( a ) = - ( v*p*D )/(2*t*E_c)`

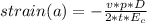
- The axial deformation in the cylinder ( δc ) becomes:

δc =
`delta ( c ) = - ( v*p*D*L_b )/(2*t*E_c)`

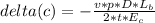
- So, the net deformation ( δ_net ) is due to the elongation of each bolts ( δb = delta ( b ) ) and contraction of cylinder ends for the amount of axial deformation ( δc = delta ( c ) ).

δ_net = δb + δc = c = T*k

- The relation becomes:

`(F_b*L_b)/(A_b*E_b) - ( v*p*D*L_b )/(2*t*E_c) = T*k\\\\p* [ (4*\pi *D^2*L_b)/(16*\pi*d_b^2 *E_b) - ( v*D*L_b )/(2*t*E_c) ] = T*k\\\\p* [ (\pi *D^2*L_b)/(4*\pi*d_b^2 *E_b) - ( v*D*L_b )/(2*t*E_c) ] = T*k\\\\`

- Now we can solve for the maximum pressure "p" allowable to prevent leakage:

`p* [ (16^2*16)/(4*(5/8)^2 *30) - ( 0.344*16*16  )/(2*0.125*16.3) ] = (1)/(2) *(1)/(16) *10^6\\\\p* [ 87.38133 - 21.61079 ] = 31250\\\\p = (31250)/(65.77054)\\\\p = 475.14 psi`

Answer: The pressure at which the cylinder will start to leak would be 475.14 psi.