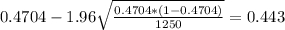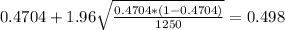Question

A survey done one year ago showed that 45% of the population participated in recycling programs. In a recent poll a random sample of 1250 people showed that 588 participate in recycling programs.

(a) Test the hypothesis that the proportion of the population who participate in recycling programs is greater than it was one year ago. Use a 5% significance level.
(b) Construct a 95% two-sided CI on the proportion

Answer 1

a)
`z=\frac{0.4704 -0.45}{\sqrt{(0.45(1-0.45))/(1250)}}=1.450`

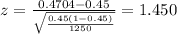
Now we can calculate the p value given by:

`p_v =P(z>1.450)=0.0735`

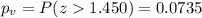
Since the p value is higher than the significance level of
`\alpha=0.05` we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that the true proportion is significantly higher than one year ago (0.45)

b)
`0.4704 -1.96 \sqrt{(0.4704*(1-0.4704))/(1250)}= 0.443`

`0.4704 +1.96 \sqrt{(0.4704*(1-0.4704))/(1250)}= 0.498`

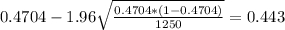
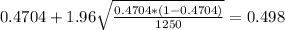
Explanation:

Information given

n=1250 represent the sample size selected

X=588 represent the people who participate in recycling programs.

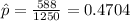`\hat p=(588)/(1250)=0.4704` estimated proportion of people who participate in recycling programs.

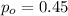`p_o=0.45` is the value to compare

`\alpha=0.05` represent the significance level

z would represent the statistic

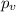`p_v` represent the p value

Part a

We want to test the hypothesis that the proportion of the population who participate in recycling programs is greater than it was one year ago (0.45):

Null hypothesis:
`p\leq 0.45`

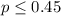
Alternative hypothesis:
`p > 0.45`

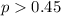
The statistic would be given by:

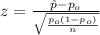`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info given we got:

`z=\frac{0.4704 -0.45}{\sqrt{(0.45(1-0.45))/(1250)}}=1.450`

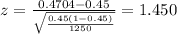
Now we can calculate the p value given by:

`p_v =P(z>1.450)=0.0735`

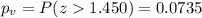
Since the p value is higher than the significance level of
`\alpha=0.05` we have enough evidence to FAIL to reject the null hypothesis and we can't conclude that the true proportion is significantly higher than one year ago (0.45)

Part b

the confidence interval would be given by:

`\hat p \pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

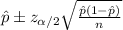
And the critical value for a 95% confidence interval can be obtained in the normal distribution and we got
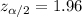`z_(\alpha/2) =1.96`. And replacing into the confidence interval formula we got:

`0.4704 -1.96 \sqrt{(0.4704*(1-0.4704))/(1250)}= 0.443`

`0.4704 +1.96 \sqrt{(0.4704*(1-0.4704))/(1250)}= 0.498`