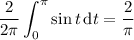Question

Given v(t) = sint , calculate the average velocity from t = 0 seconds to t = 2


`\pi`
seconds. Then calculate the average speed for the same interval.​

Answer 1

The average velocity over the interval [0, 2π] is equal to the average value of v (t ) over the same interval:

`\displaystyle\frac1{2\pi-0}\int_0^(2\pi)v(t)\,\mathrm dt=0`

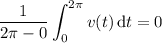
(since sin(t ) has a period of 2π)

Speed is the magnitude of velocity, or |v (t )| (the absolute value of v ). So the average speed over [0, 2π] is

`\displaystyle\frac1{2\pi-0}\int_0^(2\pi)|\sin t|\,\mathrm dt`

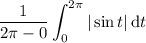
sin(t ) is positive for t between 0 and π, and negative between π and 2π. So the integral above is equal to

`\displaystyle\frac1{2\pi}\left(\int_0^\pi\sin t\,\mathrm dt+\int_\pi^(2\pi)(-\sin t)\,\mathrm dt\right)`

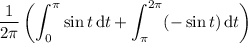
Recall that sin(t - π) = -sin(t ), so the above becomes

`\displaystyle\frac1{2\pi}\left(\int_0^\pi\sin t\,\mathrm dt+\int_\pi^(2\pi)\sin(t-\pi)\,\mathrm dt\right)`

Replacing t - π with t shifts the interval of integration for the second integral to [0, π], so really we end up with

`\displaystyle\frac2{2\pi}\int_0^\pi\sin t\,\mathrm dt=\frac2\pi`