Answer:
Check the explanation
Explanation:
Given that;
93% of students in Mrs Muratore's Ap Statistics class turn in their assignments on time,85% of Mrs Muratore's AP statistics students turn in their assignments with every problem completed,and 80% of Mrs Muratore's AP statistics students turn in their assignments on time and with every question completed
a)Let A be the event of class turn their assignment on time and B be the event class turn in their assignments with every problem complete.

b)
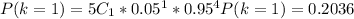
c)If there are 70 students, P(complete &time)=0.8
N(complete and time)=70*0.8
N(complete and time) =56
d)We can assume a normal distribution with mean=70*0.93=65.1 and variance=70*0.93*.07=4.557 and simulate random numbers to see the number of people who would turn an assignment in on time.
We can cap the simulation output to 70 an count the number of outputs that are atleast 68 and divide it by the total number of outputs.