Question

93% of students in Mr. Adkins AP statistics class turn in their assignments on time, 85% of Mr. Adkins AP statistics students turn in their assignments with every problem completed, and 80% of Mr. Adkins AP statistics students turn in their assignments on time and with every question completed. Assume that assignment submissions are independent.

(a) Given that a randomly selected assignment is turned in late, what is the probability that every problem was completed?
(b) If Mr. Adkins randomly selects student assignments one at a time, what is the probability that it the first assignment he finds that is not turned in on time with every question completed is one of the first 5 selected?
(c) Mr. Adkins has 70 total AP statistics students. Describe the distribution of the proportion of papers that are turned in complete and on time for a randomly chosen assignment.
(d) Explain how you would conduct a simulation to estimate the probability that at least 68 of Mr. Adkins 70 AP statistics students would turn an assignment in on time.

Answer 1

Check the explanation

Explanation:

Given that;

93% of students in Mrs Muratore's Ap Statistics class turn in their assignments on time,85% of Mrs Muratore's AP statistics students turn in their assignments with every problem completed,and 80% of Mrs Muratore's AP statistics students turn in their assignments on time and with every question completed

a)Let A be the event of class turn their assignment on time and B be the event class turn in their assignments with every problem complete.

`P(Late)=1-0.93P(Late)=0.07 \\ P(Late\, and\, not \, completed)=1-(0.93+0.85-0.8)\\ P(Late\, and\, not \, completed)=1-0.98 \\ P(Late\, and\, not \, completed)=0.02\\ P(Late\, and\, \, completed)=1-0.02-0.93\\ P(Late\, and\, \, completed)=0.05\\ P(Late\, and\, \, completed)=5\%`

b)

`P(k=1)=5C_1*0.05^1*0.95^4P(k=1)=0.2036`

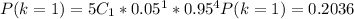
c)If there are 70 students, P(complete &time)=0.8

N(complete and time)=70*0.8

N(complete and time) =56

d)We can assume a normal distribution with mean=70*0.93=65.1 and variance=70*0.93*.07=4.557 and simulate random numbers to see the number of people who would turn an assignment in on time.

We can cap the simulation output to 70 an count the number of outputs that are atleast 68 and divide it by the total number of outputs.