Answer:
- Solution of equation ( q ) = 16
Explanation:
In this question we have given an equation that is 3 ( q - 7 ) = 27 and we have asked to solve this equation that means to find the value of q .
Solution : -
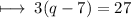
Step 1 : Solving parenthesis :
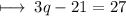
Step 2 : Adding 21 on both sides :
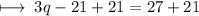
On further calculations we get :
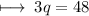
Step 3 : Dividing by 3 from both sides :
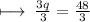
On further calculations we get :
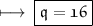
- Therefore, solution of equation ( q ) is 16 .
Verifying : -
Now we are very our answer by substituting value of q in the given equation . So ,
Therefore, our solution is correct .
#Keep Learning