Question

The mean consumption of water per household in a city was 1425 cubic feet per month. Due to a water shortage because of a drought, the city council campaigned for water use conservation by households. A few months after the campaign was started, the mean consumption of water for a sample of 100 households was found to be 1175 cubic feet per month. The population standard deviation is given to be 250 cubic feet.

A. Find the p-value for the hypothesis test that the mean consumption of water per household has decreased due to the campaign by the city council. Would you reject the null hypothesis at α = .025?

B. Make the test of part A using the critical-value approach and α = .025

Answer 1

a)
`t=(1175-1425)/((250)/(√(100)))=-10`

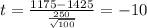
The degrees of freedom are given by:

`df=n-1=100-1=99`

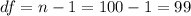
The p value for this case would be given by:

`p_v =P(t_(99)<-10) \approx 0`

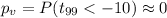
Since the p value is significantly lower than he significance level given we have enough evidence to reject the null hypothesis and we can conclude that the true mean is lower than 1425

b) For this case we need to find a critical value in the t distribution with 99 degrees of freedom who accumulates 0.025 of the area in the right tail and we got:

`t_(\alpha/2)=1.984`

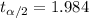
Since the calculated value is higher than the critical value we can reject the null hypothesis at the significance level provided and we can say that the true mean is higher than 1425

Explanation:

Information given

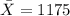`\bar X=1175` represent the sample mean for the cubic feets of households

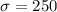`\sigma=250` represent the population standard deviation

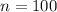`n=100` sample size

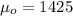`\mu_o =1425` represent the value to verify

`\alpha=0.025` represent the significance level

t would represent the statistic

`p_v` represent the p value

Part a

We want to test that the mean consumption of water per household has decreased due to the campaign by the city council, the system of hypothesis would be:

Null hypothesis:
`\mu \geq 1425`

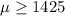
Alternative hypothesis:
`\mu < 1425`

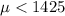
Since we don't know the deviation the statistic is given by:

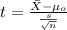`t=(\bar X-\mu_o)/((s)/(√(n)))` (1)

The statistic is given by:

`t=(1175-1425)/((250)/(√(100)))=-10`

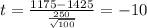
The degrees of freedom are given by:

`df=n-1=100-1=99`

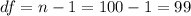
The p value for this case would be given by:

`p_v =P(t_(99)<-10) \approx 0`

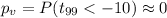
Since the p value is significantly lower than he significance level given we have enough evidence to reject the null hypothesis and we can conclude that the true mean is lower than 1425

Part b

For this case we need to find a critical value in the t distribution with 99 degrees of freedom who accumulates 0.025 of the area in the right tail and we got:

`t_(\alpha/2)=1.984`

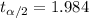
Since the calculated value is higher than the critical value we can reject the null hypothesis at the significance level provided and we can say that the true mean is higher than 1425