Question

Luc, who is 1.80 m tall and weighs 950 N, is standing at the center of a playground merry-go-round with his arms extended,

holding a 4.0 kg dumbbell in each hand. The merry-go-round can be modeled as a 4.0-m-diameter disk with a weight of 1500 N.Luc’s body can be modeled as a uniform 40-cm-diameter cylinder with massless arms extending to hands that are 85 cm from his center. The merry-go round is coasting at a steady 35 rpm when Luc brings his hands in to his chest. Afterward,what is the angular velocity, in rpm, of the merry-go-round?

Answer 1

Use the conservation of angular momentum of the entire system.

`L=Iw\\L_i=L_f`

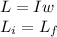
L=angular momentum

I=inertia

w=angular velocity

m_d=mass of dbell (it wouldn't let me type the whole word lol)

m_w=mass of merry-go-round

m_L=mass of Luc

r= radius (subscripts will match the masses' subscripts)

The initial angular momentum can be written as follows.

`L_i=w_i(0.5*m_L*r_L^2+2[m_d*r_d^2]+0.5*m_w*r_w^2)`

Here, I treated the dbells as a particle and went ahead and added the two together (thus the factor of 2 in front). Luc and the merry-go-round can both be modeled as cylinders. Also, I expanded inertia into I=mr^2 incase you are wondering where the I went to. Next, we need to find the final angular momentum.

`L_f=w_f(0.5*m_L*r_L^2+2[m_d*r_L^2]+0.5*m_w*r_w^2)`

As you can see, the only thing that changed was where the dbells are at. They can now be modelled as having the radius of Luc because they are at his chest. Finally we set these two equations equal to each other and solve for the final angular velocity.

`w_f=(w_i(0.5*m_L*r_L^2+2[m_d*r_d^2]+0.5*m_w*r_w^2))/(0.5*m_L*r_L^2+2[m_d*r_L^2]+0.5*m_w*r_w^2)`

From here it is plug and chug. To save myself time, I will just give you the answer. You can plug the numbers in yourself. Make sure when you plug in the numbers you convert everything into kilograms (just divide Newton's by gravity to get kg) and meters, but you can leave rpm in rpm since we are looking for an answer with rpm.

`w_f=35.6 rpm`

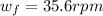
P.S. Please double check that number. I am 99.9% positive the equation is right because I just did a similar problem and got the right answer using that equation, but my numbers were different. So, just double check by plugging the numbers into the calculator yourself. I could have made a small calculator mistake when plugging it in, but I do think it should be right.

Answer 2

The angular velocity is
`w_f = 35.6\ rpm`

Step-by-step explanation:

From the question we are told that

The height of Luc is
`h = 1.80 \ m`

The weight of Luc is
`W = 950 \ N`

The mass of the dumbbell is
`m_b = 4.0 \ kg`

The diameter of the merry-go-round is
`d_1 = 4 m`

The diameter of the merry-go-round is
`r_1 = (4)/(2) = 2 m`

The distance of the hand from the center is
`L = 85cm = (85)/(100) = 0.85\ m`

The diameter of Luc is
`d_2 = 40 c m = (40)/(100) = 0.4 m`

The diameter of the merry-go-round is
`r_1 = (0.4)/(2) =0. 2 m`

The weight of the merry-go round is
`W_m = 1500 \ N`

The steady speed of the merry go round is
`w_i = 35 rpm = 35 * (2 \pi )/(60) = 3.66 rad/s`

Generally the moment of inertia before Luc brings his hand to his chest is mathematically represented as

`I_i = (m_b * r _1^2)/(2 ) + (m_m * r^2_2)/(y) + 2 * m_b L^2`

Where
`m_m` is the mass of the merry-go round which is

`m_m = (1500)/(9.8) = 150 kg`

`m` is the mass of Luc which is

`m_m = (950)/(9.8) = 95 kg`

`m_b` is the mass of dumbell which is

`m_m = (950)/(9.8) = 95 kg`

So

`I_i = (150 * 2^2)/(2) + (95 * 0.2^2)/(2) + 2 * 4 * (0.85)^2`

`I_i = 307 .7 \ kg \cdot m^2`

The moment of inertia after Luc brings his hand to his chest is mathematically represented as

`I _2 = (m_b * r _1^2)/(2 ) + (m_m * r^2_2)/(y)`

Substituting value

`I _2 = (150 * 2^2 )/(2 ) + ( 95 * (0.2) ^2)/(2)`

`I _2 = 302 \ kg \cdot m^2`

According to the law of conservation of angular momentum

`w_f I_f = w_i I_i`

`w_f = ( w_i I_i)/(I_f)`

Substituting values

`w_f = (3.66 * 307.7)/(302)`

`w_f =3.73 \ rad/s`

Converting back to rpm

`w_f =3.73 * (60)/(2 \pi)`

`w_f = 35.6\ rpm`