Question

You have just put some medical eyedrops on your sensitive eyes. The cornea has an index of refraction of 1.38, while the eye drops have a refractive index of 1.45. After you put in the drops, your friends notice that your eyes look red, becuase red light of a wavelength of 600 nm has been reinforced in the reflected light.

(a) What is the minimum thickness of the film of eyedrops on your cornea?

(b) Will any other wavelengths of visible light be reinforced in the reflected light? Will any be cancelled?

(c) Suppose you had contact lenses, so that the eyedrops went on them instead of your corneas. If the refractive index of the lens material is 1.50 and the layer of eyedrops has the same thickness in part (a), what wavelengths of visible light will be reinforced? What wavelengths will be cancelled?

Answer 1

a) t = 1.03 10⁻⁻⁷ m , b) NO OTHER λ REINFORCED, c) NO WAVE LENGTHS TO BE REINFORCED

Step-by-step explanation:

In reflection interference we must take into account two things:

* when the light passes through a medium with a lower index of refraction to one with a higher index, it undergoes a phase change of 180º

* Wavelength changes as it passes through a medium

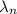`\lambda_(n)`= λ / n

taking into account these two aspects the relationship for constructive interference is

2 t = (m + ½) λ / n

where t is the thickness of the film, n the drop index and m an integer

a) they ask us for the minimum thickness

in this case m = 0

2t = ½ λ / n

we calculate

t = ¼ 600 10⁻⁹ / 1.45

t = 1.03 10⁻⁻⁷ m

b) that other wavelengths are reinforced, for the same thickness

λ = 2 n t / (m + ½)

we substitute

λ= 2 1.45 1.03 10⁻⁷ / (m + ½)

λ = 2,987 10⁻⁷ / (m + ½)

we look for the wavelengths in the visible range that goes from 400 nm to 700 nm,

for which we give values ​​to m

for m = 1

λ = 2,987 10⁻⁷ / (1+ ½)

λ = 1.99 10⁻⁷ m

we reduce to nm

λ = 199 nm

is outside the visible range

for m = 2

λ = 2,987 10⁻⁷ (2 + ½)

λ = 1.19 10⁻⁷ m = 119 nm

we can see that when increasing the value of the integer the wavelength moves away from the visible range, so there are NO OTHER REINFORCED λ

c) in this case we see that there is a phase change of 180º between the interface house : air - drop and between drops - lens

¹

consequently the constructive interference formula remains

2t = (m +1) λ / n

if we change m + 1 = m ’, we have

2t = m’ λ / n

m’ = 1, 2, 3, ...

λ = 2 n t / m ’

we substitute

λ = 2 1.45 1.03 10⁻⁷ / m ’

λ = 2,987 10⁻⁷ / m ’

we give values ​​to m ’ to find the wavelengths in the visible range

m’= 1 λ = 2,987 10⁻⁷ m = 298.7 nm

this in the ultraviolet

m’= 2 λ = 2,987 10⁻⁷ / 2 = 1.49 10⁻⁷ m = 147 nm

we see that there are NO WAVE LENGTHS TO BE REINFORCED

all wavelengths are canceled