Question

Bacteria can multiply at an alarming rate when each bacteria splits into two new cells, thus doubling. If we start with only one bacteria which can double every hour, how many bacteria will we have by the end of one day? Show your work.

Answer 1

`y = a(b)^t`

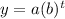
Where a =1 represent the initial amount of bacteria and b =2 represent the growth factor, for this case since each hour we double the number of bacteria for this reason b =2. And t represent the number of hours after the first bacteria is founded.

So then our model would be given by:

`y = 1 (2)^t`

And since we want to find the number of bacteria at the end of one day, and we know that one day = 24 hours we can replace the value of t =24 into the model and we got:

`f(24) = 1 (2)^(24)=16777216`

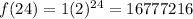
Then we can conclude that at the end of the day we would expect 16777216 bacteria

Explanation:

For this case we can use the exponential model given by this general expression:

`y = a(b)^t`

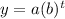
Where a =1 represent the initial amount of bacteria and b =2 represent the growth factor, for this case since each hour we double the number of bacteria for this reason b =2. And t represent the number of hours after the first bacteria is founded.

So then our model would be given by:

`y = 1 (2)^t`

And since we want to find the number of bacteria at the end of one day, and we know that one day = 24 hours we can replace the value of t =24 into the model and we got:

`f(24) = 1 (2)^(24)=16777216`

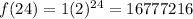
Then we can conclude that at the end of the day we would expect 16777216 bacteria