Answer:
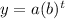
Where a =1 represent the initial amount of bacteria and b =2 represent the growth factor, for this case since each hour we double the number of bacteria for this reason b =2. And t represent the number of hours after the first bacteria is founded.
So then our model would be given by:
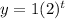
And since we want to find the number of bacteria at the end of one day, and we know that one day = 24 hours we can replace the value of t =24 into the model and we got:
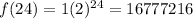
Then we can conclude that at the end of the day we would expect 16777216 bacteria
Explanation:
For this case we can use the exponential model given by this general expression:
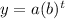
Where a =1 represent the initial amount of bacteria and b =2 represent the growth factor, for this case since each hour we double the number of bacteria for this reason b =2. And t represent the number of hours after the first bacteria is founded.
So then our model would be given by:
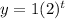
And since we want to find the number of bacteria at the end of one day, and we know that one day = 24 hours we can replace the value of t =24 into the model and we got:
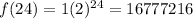
Then we can conclude that at the end of the day we would expect 16777216 bacteria