Question

"Carbon 14 (C-14), a radioactive isotope of carbon, has a half-life of 5730 ± 40 years. Measuring the amount of this isotope left in the remains of animals and plants is how anthropologists determine the age of samples. Example: The skeletal remains of the so-called Pittsburgh Man, unearthed in Pennsylvania, had lost 82% of the C-14 they originally contained. Determine the approximate age of the bones assuming a half-life of 5730."

Answer 1

The age of the bones is approximately 14172 years.

Step-by-step explanation:

The age of the bones can be determinated using the following decay equation:

`N_((t)) = N_(0)e^(-\lambda t)` (1)

Where:

N(t): is the quantity of C-14 at time t

No: is the initial quantity of C-14

λ: is the decay rate

t: is the time

First, we need to find λ:

`\lambda = (ln(2))/(t_(1/2))`

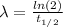
Where:

t(1/2): is the half-life of C-14 = 5730 y

`\lambda = (ln(2))/(5730 y) = 1.21 \cdot 10^(-04) y^(-1)`

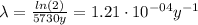
Now, we can calculate the age of the bones by solving equation (1) for t:

`t = (-ln((N_((t)))/(N_(0))))/(\lambda)`

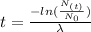
We know that the bones have lost 82% of the C-14 they originally contained, so:

`N_(t) = (1 - 0.82)N_(0) = 0.18N_(0)`

`t = (-ln(0.18))/(1.21 \cdot 10^(-04) y^(-1))`

`t = 14172 y`

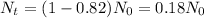
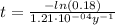
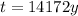
Therefore, the age of the bones is approximately 14172 years.

I hope it helps you!