To find how many terms of this sequence must be added to get 1440, we must know the arithmetic sequence equation to find any term in the sequence:
⇒
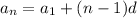
 --> value of the nth number of the sequence
--> value of the nth number of the sequence
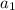 --> first term of the sequence
--> first term of the sequence- n --> position of the nth term
- d --> common difference
Let's examine the information given:
⇒
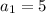
⇒ d = 2
Therefore the equation for finding the nth term of the sequence so far is:

Now we want to find how many terms this sequence must be added to get 1440
General equation for adding all the terms =
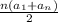
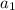 : first term of the sequence
: first term of the sequence
 : last term of the sequence
: last term of the sequence
- n: number of terms in the sequence.
Using all the information given, let's plug in the all the values:

To solve this we set (2n + 80) = 0 and (n-36) = 0
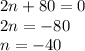
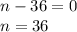
In this case, n can only equal 36 since n cannot be negative.
Answer: 36 terms of this sequence must be added to get 1440.
Hope that helps!