Question

A movie theater has a seating capacity of 163. The theater charges $5.00 for children, $7.00 for students,

and $12.00 of adults. There are half as many adults as there are children. If the total ticket sales was $
1170, How many children, students, and adults attended?
children attended.
students attended.
adults attended.

Answer 1

58 children , 29 adults and 76 students attended the theater

Explanation:

Let x be the number of children

We are given that There are half as many adults as there are children.

So, Number of adults =
`(1)/(2)x`

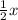
Let y be the no. of students

A movie theater has a seating capacity of 163.

So,
`x+(x)/(2)+y=163`

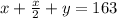
2x+x+2y=326

3x+2y=326 ----1

The theater charges $5.00 for children, $7.00 for students, and $12.00 of adults.

Cost of x tickets of children = 5x

Cost
`(x)/(2)` tickets of adults =
`12 * (x)/(2)=6x`

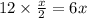
Cost of y tickets of students = 7y

The total ticket sales was $ 1170

So, 5x+6x+7y=1170

11x+7y=1170 ----2

Plot equation 1 and 2

3x+2y=326 --- Black line

11x+7y=1170 --- red line

Intersection point will give the solution.

Intersection point =(x,y)=(58,76)

Number of children attended = 58

Number of adults attended =
`(58)/(2)=29`

Number of students attended = 76

Hence 58 children , 29 adults and 76 students attended the theater