Answer:
107.1° C
Step-by-step explanation:
The properties of air from table '' properties of air at 1 atm pressure'' recorded at temperature T = 50°C
Thermal conductivity k = 0.02735 W/m.K
Kinematic viscosity v = 1.798 × 10⁻⁵ m²/s
Prandtl number Pr = 0.7228
Determine the characteristics length , L

where;
x represent the length of the chip
E represent the unheated stating length
Replacing 15 mm for x and 15 mm for E
L = 15 + 15
L = 30 mm
To calculate the Reynolds number for the flow at the trailing edge (x = L + E)
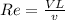
Here;
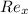 is the Reynolds number and L is the characteristics length
is the Reynolds number and L is the characteristics length
Replacing 23.4 m/s for V , 30 mm for L and 1.798 × 10⁻⁵ m²/s for v
Re =
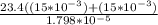
Re = 20355.95106
Thus, since the obtained Reynolds number is less than
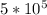 i.e Re <
i.e Re <
To Calculate the local Nusselt number
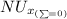 for the laminar flow with uniform heat flux ; we have :
for the laminar flow with uniform heat flux ; we have :
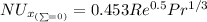
Replacing 20355.95106 for Re and 0.7228 for Pr; we get:


Calculate the Nusselt number for the silicon chip whose edges are flush in substrate
![Nu_x = \frac{NU_{x_(( \sum = 0) )}}{[1-( E/L)^(3/4)]^(1/3)}](https://img.qammunity.org/2021/formulas/engineering/college/jcgkss69pg5cl87uyz7lgwsbavshnbrtxc.png)
Replacing
 , 30 mm for L and 15 mm for E
, 30 mm for L and 15 mm for E
![Nu_x = (58.0)/([1-( 15*10^(-3)/0.03)^(3/4)]^(1/3))](https://img.qammunity.org/2021/formulas/engineering/college/ca7k0z1l6xlgq543hepzd67yhepsaffulz.png)
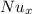 = 78.37
= 78.37
To the determination of the local heat coefficient
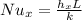
making
 the subject of the formula
the subject of the formula
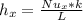
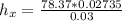
= 71.44 W/m² . K
Considering Newton's Law of cooling and calculating for the surface temperature; we have:

making
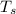 the subject of the formula
the subject of the formula
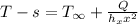
where Q = heat transfer = 1.4 W
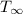 = ambient temperature 20° C
= ambient temperature 20° C
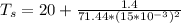
= 107.1° C
Thus, the surface temperature at the trailing edge of the chip is = 107.1° C