Answer:
Probability that a person actually has the disease given that the test indicates the presence of the disease is 0.657.
Explanation:
We are given that a blood test indicates the presence of a particular disease 95% of the time when the disease is actually present.
The same test indicates the presence of the disease 0.5% of the time when the disease is not actually present. One percent of the population actually has the disease.
Let the Probability that person actually has the disease = P(A) = 0.01
Probability that person actually doesn't has the disease = P(A') = 1 - P(A) = 1 - 0.01 = 0.99
Also, let PD = event that there is a presence of the disease
So, Probability that test indicates the presence of the disease given the fact that the disease is actually present = P(PD/A) = 0.95
Probability that test indicates the presence of the disease given the fact that the disease is not actually present = P(PD/A') = 0.005
Now, the probability that a person actually has the disease given that the test indicates the presence of the disease = P(A/PD)
We will use Bayes' theorem to calculate the above probability.
SO, P(A/PD) =
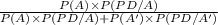
=

=
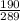 = 0.657
= 0.657
Hence, the required probability is 0.657.