Answer:
There are 3 sub answers from the above question.
1. the time the heat pump ran that day = 89,495.7726 ÷ 4.8 = 18,645 seconds or 310.75 minutes or 5.18 hours
2.Cost= (4.8 x 5.18) x 11 = 273.5 g (We assume in the question that the "g" signifies currency).
3. New cost = 4,033.33 g (We assume in the question that the "g" signifies currency).
Step-by-step explanation:
1. To find how long the heat pump ran on that day, we have to look at the coefficient of performance of the pump. This will then enable us find the work done by the heat pump.
Coefficient of performance of the heat pump, C
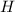 = 1 ÷ ( (1 - (TL ÷ TH) )
= 1 ÷ ( (1 - (TL ÷ TH) )
Heated space, TH = 22°C = 295k
Out door air temperature, TL = 2 °C = 275k
where, 1°C = 273k
= 1 ÷ ( (1 - ( 275k ÷ 295k) )
C
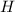 = 14.7493
= 14.7493
Then the work done by the heat pump
W = QH ÷ CH
Where, the rate of heat loses, Q
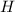 given = 55,000 kJ/h
given = 55,000 kJ/h
= (55,000 x 24) ÷ 14.7493 = 89,495.7726 kJ
Where, 24 is the number of hours in a day
Therefore, the time the heat pump ran that day = the work done by the heat pump ÷ the power the heat pump consumes during operation
the time the heat pump ran that day = 89,495.7726 ÷ 4.8 = 18,645 seconds or 310.75 minutes or 5.18 hours
2. To find the total heating costs assuming an average price of electricity of 11 g/kWh.
In the question "g" signifies currency.
Therefore,
cost = (the power the heat pump consumes during operation x the time in hours the heat pump ran that day) x price in g
Cost= (4.8 x 5.18) x 11 = 273.5 g
3. To find the heating cost for the same day if resistance heating is used instead of a heat pump.
If the resistance heating was used, the cost will be:
New cost = the rate of heat loses x price in g
New cost = ( (55,000 x 24) ÷ 3600) ) x 11
New cost = 4,033.33 g
Where, 24= hours in a day
and, 3600 = seconds in one hour