Answer:
The probability of the system being down in the next hour of operation is 0.3.
Explanation:
We have a transition matrix from one period to the next (one hour) that can be written as:
![T=\left[\begin{array}{ccc}&R&D\\R&0.7&0.3\\D&0.2&0.8\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/fv76nzs4cd6qs790ukemjgr12kfwkjbgc9.png)
We can represent the state that system is initially running with the vector:
![S_0=\left[\begin{array}{cc}1&0\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/a06bxx8mixp1bxxyy9si0783dl6gusjjlf.png)
The probabilties of the states in the next period can be calculated using the matrix product of the actual state and the transition matrix:
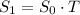
That is:
![S_1=S_0\cdot T= \left[\begin{array}{cc}1&0\end{array}\right]\cdot \left[\begin{array}{cc}0.7&0.3\\0.2&0.8\end{array}\right]= \left[\begin{array}{cc}0.7&0.3\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/v98ndjsbzxkbklicmdol3bkwzis7sqc75m.png)
With the inital state as running, we have a probabilty of 0.7 that the system will be running in the next hour and a probability of 0.3 that it will be down.