Question

When network cards are communicating, bits can occasionally be corrupted in transmission. Engineers have de- termined that the number of bits in error follows a Poisson dis- tribution with mean of 3.2 bits/kb (per kilobyte). (a) What is the probability of 5 bits being in error during the transmission of 1 kb? (b) What is the probability of 8 bits being in error during the transmission of 2 kb? (c) Whatistheprobabilityofnoerrorbitsin3kb?

Answer 1

a) 11.40% probability of 5 bits being in error during the transmission of 1 kb

b) 11.60% probability of 8 bits being in error during the transmission of 2 kb

c) 0.01% probability of no error bits in 3kb

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the giveninterval.

Poisson distribution with mean of 3.2 bits/kb (per kilobyte).

This means that
`\mu = 3.2kb`, in which kb is the number of kilobytes.

(a) What is the probability of 5 bits being in error during the transmission of 1 kb?

This is P(X = 5) when
`\mu = 3.2`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 5) = (e^(-3.2)*3.2^(5))/((5)!) = 0.1140`

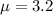
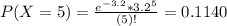
11.40% probability of 5 bits being in error during the transmission of 1 kb

(b) What is the probability of 8 bits being in error during the transmission of 2 kb?

This is P(X = 8) when
`\mu = 2*3.2 = 6.4`

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 8) = (e^(-6.4)*6.4^(8))/((8)!) = 0.1160`

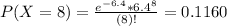
11.60% probability of 8 bits being in error during the transmission of 2 kb

(c) What is the probability of no error bits in 3kb?

This is P(X = 0) when
`\mu = 3*3.2 = 9.6`

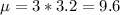
Then

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-9.6)*9.6^(0))/((0)!) = 0.0001`

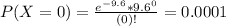
0.01% probability of no error bits in 3kb