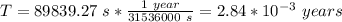Question

Suppose that scientists discover an asteroid that is 2.0 AU from the sun. If 1 AU - 150 million km, how long would the asteroid's orbital period be in Earth years?

Answer 1

2.84*10^-3 years = 0.00284*10^-3 years

Step-by-step explanation:

To find the orbital period you use the following formula:

`T=\sqrt{(4\pi^2r^3)/(GM)}`

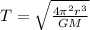
r: 2.0A = 2.0(1.5*10^11m)=3*10^11 m

G: Cavendish constant = 6.67*10^-11 Nm^2/kg^2

M: mass of the sun = 1.98*10^30 kg

`T=\sqrt{(4\pi^2(3*10^(11)m)^3)/((6.67*10^(-11)Nm^2/kg^2)(1.98*10^(30)kg))}\\\\T=89839.27\ s`

Next, you calculate the time in seconds of one Earth's year:

`1\ year=365days*(24\ h)/(1\ day)*(3600\ s)/(1\ h)=31536000\ s`

thus, you use this value to find the orbital period of the asteroid in Earth's year:

`T=89839.27\ s*(1\ year)/(31536000\ s)=2.84*10^(-3)\ years`