Question

Eighteen percent of U.S.-based multinational companies provide an allowance for personal long-distance calls for executives living overseas, according to the Institute for International Human Resources and the National Foreign Trade Council. Suppose a researcher thinks that U.S.-based multinational companies are having a more difficult time recruiting executives to live overseas and that an increasing number of these companies are providing an allowance for personal long-distance calls to these executives to ease the burden of living away from home. To test this hypothesis, a new study is conducted by contacting 376 multinational companies. Twenty-two percent of these surveyed companies are providing an allowance for personal long-distance calls to executives living overseas. Does the test show enough evidence to declare that a significantly higher proportion of multinational companies provide a long-distance call allowance? Let α = .01.

Answer 1

No, the test doesn't show enough evidence to declare that a significantly higher proportion of multinational companies provide a long-distance call allowance.

Explanation:

We are given that Eighteen percent of U.S.-based multinational companies provide an allowance for personal long-distance calls for executives living overseas.

A new study is conducted by contacting 376 multinational companies. Twenty-two percent of these surveyed companies are providing an allowance for personal long-distance calls to executives living overseas.

Let p = proportion of multinational companies who provide a long-distance call allowance.

So, Null Hypothesis,
`H_0` : p
`\leq` 18% {means that lesser or same proportion of multinational companies provide a long-distance call allowance}

Alternate Hypothesis,
`H_0` : p > 18% {means that higher proportion of multinational companies provide a long-distance call allowance}

The test statistics that would be used here One-sample z proportion statistics;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of companies who are providing an allowance for personal long-distance calls = 22%

n = sample of multinational companies = 376

So, test statistics =
`\frac{0.22-0.18}{\sqrt{(0.22(1-0.22))/(376) } }`

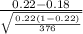
= 1.872

The value of z test statistics is 1.872.

Now, at 0.01 level of significance the z table gives critical value of 2.3263 for right-tailed test. Since, our test statistics is less than the critical value of z as 1.872 < 2.3263, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that lesser or same proportion of multinational companies provide a long-distance call allowance.