Corrected Question
The graphs below shows some properties of regular polygons. When compared with the independent variable, how many of the other three columns of the graphs represent a linear relationship?
(A)0 (B)1 (C)2 (D)3
Answer:
(C)2
Explanation:
Given the independent variable (Number of sides of the polygon), we notice that out of the three other columns:
Number of Diagonals
- Slope=
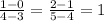
Sum of all interior angles
- Slope=
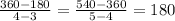
Measure of each angle
- Slope=
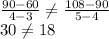
Therefore, the measure of each angle does not represent a linear relationship.
Only 2 columns represent a linear relationship.
The correct option is C.
See below for the table