Question

Find the volume of the regular hexagonal prism below.

Answer 1

B. 179.1 cm3

Explanation:

sorry if i get it wrong

Answer 2

The volume of a regular hexagonal prism is
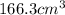`166.3cm^3`. So, the closest option is
`1. 166.3 cm^3.`

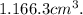
To find the volume of a regular hexagonal prism, you can use the formula:

Volume=
`(3√(3) )/(2) * side length^2 * height`

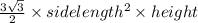
In this case, the side length of the regular hexagon is given as 4 cm, and the height of the prism is also 4 cm. Plug these values into the formula:

Volume=
`(3√(3) )/(2) * 4^2 * 4`

Volume=
`(3√(3) )/(2) * 16 * 4`

Volume=
`(3√(3) )/(2) * 64`

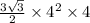
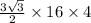
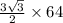
Volume=96√3

Now, you can calculate the numerical value:

Volume≈ 1
`66.3cm^3`

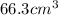
So, the closest option is 1. 166.3
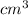
`cm^3`

​

.