Find the volume of a right circular cone that has a height of 14.7 ft and a base with a circumference of 13 ft. Round your answer to the nearest tenth of a cubic foot.

Question

asked Feb 3, 2021 85.5k views

2 Answers

Derek Lewis · Answer 1 · 2021-02-09T02:26:33+0000

Answer:

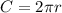
$C= 2\pi r$

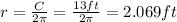
$r = (C)/(2\pi) =(13 ft)/(2\pi)= 2.069 ft$

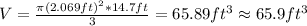
$V =(\pi (2.069 ft)^2 *14.7 ft)/(3)= 65.89 ft^3 \approx 65.9 ft^3$

So then the final answer after round to the nearest tenth is 65.9 ft^3

Explanation:

For this case we know that the volume for a right ciruclar cone is given by this formula:

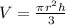
$V = (\pi r^2 h)/(3)$

Where:

represent the radius

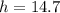h = 14.7 represent the heigth

We know the length of the circumference on this case
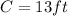C = 13 ft and by properties we know that:

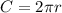
$C= 2\pi r$

Solving for r we got:

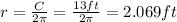
$r = (C)/(2\pi) =(13 ft)/(2\pi)= 2.069 ft$

Now replacing the value of the radius and heigth into the formula for the volume we got:

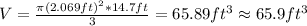
$V =(\pi (2.069 ft)^2 *14.7 ft)/(3)= 65.89 ft^3 \approx 65.9 ft^3$

So then the final answer after round to the nearest tenth is 65.9 ft^3