In case you're not already aware, the expression
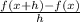 is called the "difference quotient" and represents the average rate of change of a function
is called the "difference quotient" and represents the average rate of change of a function
 over an interval
over an interval
![[x,x+h]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4x1own1vim8itz5zz4agqqkqbrnv714tg2.png) .
.
For the function
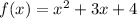 , by substituting
, by substituting
 we get
we get
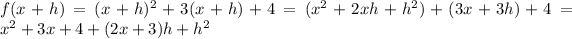
Then the difference quotient is
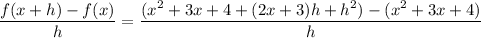
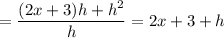
where the last equality holds as long as
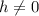 .
.