A possible leading term for the graph shown above include the following: C.
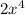 .
.
The end behavior of the graph include:
As x → +∞, then y → +∞.
As x → -∞, then y → +∞.
In Mathematics and Geometry, the degree of a polynomial function is sometimes referred to as an absolute degree and it's the greatest exponent (leading coefficient) of each of its term.
Based on the graph, the leading coefficient must be positive because the line are both pointing upward (rises to the left and right) with a multiplicity of 2 at (2, 0).
Since the leading coefficient of the above polynomial function is positive, and the degree is even, the end behavior can be described as follows;
As x tends towards positive infinity, f(x) tends towards positive infinity i.e x → ∞, f(x) → ∞.
As x tends towards negative infinity, f(x) tends towards positive infinity i.e x → -∞, f(x) → ∞.