Answer:
20.52cm^2
Explanation:
from the picutre we can see that this is a semicircle with 2 right angle triangles inside it. to find the area we will solve for the semi circle then solve for the triangles and and subtract
circle area is
 leaving the semicircle to be
leaving the semicircle to be
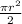 for the semi circle
for the semi circle
next we need the radius. since the diameter is given, we can solve for r by dividing it in two
12 ÷ 2 = 6
so the area of the semi circle is
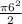
this gives 18
 cm^2 if we simplify
cm^2 if we simplify
next the triangles, since they are equal in size we can treat them as a square and stack them. this is because they have equal side lengths so when stacked they form a square:
base x height divided by 2 times 2 would be the normal process to find two equal triangles but you can see the division and multiplication cancel out
6x6= 36cm^2
finally subtracting the areas to find the shaded region and use 3.14 as pi
18
 cm^2 - 36cm^2 = 20.52cm^2
cm^2 - 36cm^2 = 20.52cm^2