Question

Write a quadratic equation in standard form that has a vertex of (-2, 6) and passes through (-4, -2).

Answer 1

The equation of the quadratic in standard form is:

`y=-2x^2-8x-2`

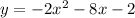
Explanation:

Since they give us the information about where the vertex of the parabola is located, and one extra points where it passes through, we can use the general form of a quadratic in vertex form:

`y-y_v=a\,(x-x_v)^2`

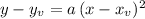
where
`(x_v,y_v)` is the location of the vertex (in our case the point (-2,6).

Therefore the equation above becomes:

`y-y_v=a\,(x-x_v)^2\\y-6=a\,(x-(-2))^2\\y-6=a\,(x+2)^2`

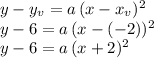
Now,we can use the fact that the point (-4,-2) is also a point of the graph, to find the value of the parameter
:

`y-6=a\,(x+2)^2\\-2-6=a\,(-4+2)^2\\-8=a\,(-2)^2\\-8=a\,*4\\a=-2`

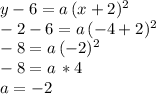
Then, the equation of the quadratic with such characteristics becomes:

`y-6=-2\,(x+2)^2\\y-6=-2x^2-8x-8\\y=-2x^2-8x-2`

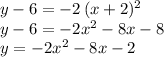
which is the equation of the quadratic in standard form.