Question

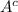If U = {all positive integers) and A = {x\x € U and x is an odd positive integer), which describes AC?

O AC = {x|x € U and is a negative integer)
O AC = {XIX e U and is zero}
O A = {x\* € U and is not an integer}
O AC = {x\% € U and is an even positive integer;

Answer 1

Answer:heyy, the correct answer would be (d) hope this helps :)

Step-by-step explanation: just took the test and got all of them correct

Answer 2

(D)
`A^c` = {x| x
`\in` U and x is an even positive integer}

Explanation:

If the Universal set, U = {all positive integers); and

A = {x|x
`\in` U and x is an odd positive integer}.

Then:

The complement of A is the set of the of the elements of the universal set which are not in A.

If a set is not odd, then it is even.

Therefore:

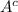`A^c` = {x| x
`\in` U and x is an even positive integer}

The correct option is D

Remark

The Universal set consists of only positive integers, therefore negative numbers are out(Option A). Similarly, Zero(0) is also out (Option B).

Likewise in option C, numbers that are not integers are not in the universal set therefore they cannot be in the complement of A.