Question

A busy, two-lane split highway crosses another busy split highway. The northbound lanes are divided from the southbound lanes by a borrow pit. To maintain a direct line of traffic flow, the lines of traffic must be parallel. To verify this, you need to prove that in the following diagram the lines of traffic are parallel.

Given :
angle CBD=angle BDH; measure of angel ABJ+measure of angle IHG=180
Prove:
line A F is parallel to line LG

Answer 1

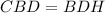`\angles CBD = \angles BDH`, by given.

Lines CK and EI are parallels, because CBD and BDH are corresponding angles.

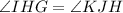`\angle IHG = \angle KJH`, by corresponding angles.

`\angle ABJ + \angle KJH = 180\°`

And,
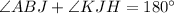
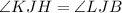`\angle KJH = \angle LJB`, by vertical angles.

So,
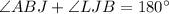`\angle ABJ + \angle LJB = 180\°`, these angles are same side internal angles. When they sum 180° means that they are between parallels.

Therefore, line A.F and LG are parallels.