Question

A (0, 2) and B (6,6) are points on the straight line ABCD.

AB = BC = CD
Work out the coordinates of D.
B (
66)
A(0,2)
Total marks: 3​

Answer 1

D: (18,14)

Explanation:

AB: < 6-0 , 6-2 >

AB: < 6 , 4 >

OD = OB + 2(AB)

OD = < 6 , 6 > + 2< 6 , 4 >

OD = < 6+12 , 6+8 >

OD = < 18 , 14 >

D: (18,14)

Answer 2

(18, 14)

Explanation:

We know that C and D lie on the line AB and BC = CD = AB. Then we need to use the distance formula and equation of the line AB to find the other two coordinates.

The distance formula states that the distance between two points
`(x_1,y_1)` and
`(x_2,y_2)`, the distance is denoted by:
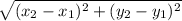`√((x_2-x_1)^2+(y_2-y_1)^2)`. Let's find the distance between A and B:

d =
`√((6-0)^2+(6-2)^2)=√(6^2+4^2) =√(36+16) =√(52) =2√(13)`

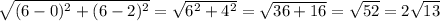
Now say the coordinates of D are (a, b). Then the distance between D and B will be twice of 2√13, which is 4√13:

4√13 =
`√((6-a)^2+(6-b)^2)`

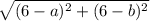
Square both sides:

208 = (6 - a)² + (6 - b)²

Let's also find the equation of the line AB. The y-intercept we know is 2, so in y = mx + b, b = 2. The slope is (6 - 2) / (6 - 0) = 4/6 = 2/3. So the equation of the line is: y = (2/3)x + 2. Since (a, b) lines on this line, we can put in a for x and b for y: b = (2/3)a + 2. Substitute this expression in for b in the previous equation:

208 = (6 - a)² + (6 - b)²

208 = (6 - a)² + (6 - (2/3a + 2))² = (6 - a)² + (-2/3a + 4)²

208 = a² - 12a + 36 + 4/9a² - 16/3a + 16 = 13/9a² - 52/3a + 52

0 = 13/9a² - 52/3a - 156

13a² - 156a - 1404 = 0

a² - 12a - 108 = 0

(a + 6)(a - 18) = 0

a = -6 or a = 18

We know a can't be negative so a = 18. Plug this back in to find b:

b = 2/3a + 2 = (2/3) * 18 + 2 = 12 + 2 = 14

So point D has coordinates (18, 14).