Answer:
The player ran 119 yards
Explanation:
The diagram below represents the problem.
The rectangular football fields is 64 yards wide and 100 yards long. A player ran the length of the diagonal.
Hence, we need to find the length of the diagonal of the rectangle.
The width, length and diagonal of the football field form a right-angled triangle, with opposite as 64 yards, adjacent as 100 yards and hypotenuse as x.
Applying Pythagoras' theorem, we have that:
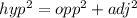
Therefore, the distance the player ran is:
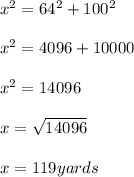
The player ran 119 yards.