Answer:
The end of the flagpole is 50.79 ft away from the base of the pole.
Explanation:
The problem is represented by the diagram below.
The broken flagpole forms the shape of a right angled triangle. We need to find one of the sides of the triangle, the adjacent (x).
The hypotenuse is the broken part of the flagpole (53 ft), while the opposite is the part of the flagpole that is still stuck to the ground (28 ft).
Using Pythagoras theorem, we have that:
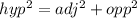
=>
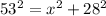
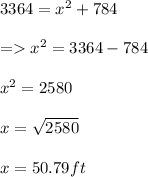
The end of the flagpole is 50.79 ft away from the base of the pole.