Question

What is an equation of the line that passes through the points (-3,8) and (-2,3)?

Answer 1

y = -5x + 7

Explanation:

You want to find the equation for a line that passes through the two points:

• (-3,8) and (-2,3)

First of all, remember what the equation of a line is:

• y = mx+b

Where:

• m is the slope, and
• b is the y-intercept

First, let's find what m is, the slope of the line...

The slope of a line is a measure of how fast the line "goes up" or "goes down". A large slope means the line goes up or down really fast (a very steep line). Small slopes means the line isn't very steep. A slope of zero means the line has no steepness at all; it is perfectly horizontal.

For lines like these, the slope is always defined as "the change in y over the change in x" or, in equation form:

`m=(y_(2) -y_(1) )/(x_(2) -x_(1) )`

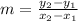
So what we need now are the two points you gave that the line passes through. Let's call the first point you gave, (-3,8), point #1, so the x and y numbers given will be called x₁ and y₁. Or x₁ = -3 and y₁ = 8.

Also, let's call the second point you gave, (-2,3), point #2, so the x and y numbers here will be called x₂ and y₂. Or, x₂ = -2 and y₂ = 3.

Now, just plug the numbers into the formula for m above, like this:

`m=(3-8)/(-2--3)`

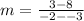
or...

`m=(-5)/(1)`

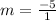
or...

`m=-5`

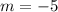
So, we have the first piece to finding the equation of this line, and we can fill it into y=mx+b like this:

`y=-5x+b`

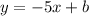
Now, what about b, the y-intercept?

To find b, think about what your (x,y) points mean:

• (-3,8). When x of the line is -3, y of the line must be 8.
• (-2,3). When x of the line is -2, y of the line must be 3.

Because you said the line passes through each one of these two points, right?

Now, look at our line's equation so far: y=-5x+b. b is what we want, the -5 is already set and x and y are just two "free variables" sitting there. We can plug anything we want in for x and y here, but we want the equation for the line that specfically passes through the two points (-3,8) and (-2,3).

So, why not plug in for x and y from one of our (x,y) points that we know the line passes through? This will allow us to solve for b for the particular line that passes through the two points you gave!

You can use either (x,y) point you want..the answer will be the same:

• (-3,8). y=mx+b or 8=-5 × -3+b, or solving for b: b=8-(-5)(-3). b=-7.
• (-2,3). y=mx+b or 3=-5 × -2+b, or solving for b: b=3-(-5)(-2). b=-7.

See! In both cases we got the same value for b. And this completes our problem.

The equation of the line that passes through the points

(-3,8) and (-2,3)

is

y=-5x-7