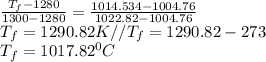Question

A closed, rigid tank fitted with a paddle wheel contains 1.8 kg of air, initially at 200 °C, 1 bar. During an interval of 15 minutes, the paddle wheel transfers energy to the air at a rate of 1 kW. During this time interval, the air also receives energy by heat transfer at a rate of 0.5 kW. These are the only energy transfers. Assume the ideal gas model for the air, and no overall changes in kinetic or potential energy. Do not assume specific heats are constant.

Determine the change in specific internal energy for the air, in kJ/kg, and the final temperature of the air, in °C.

Answer 1

a) change in specific internal energy for the air, Δu = 675 kJ

b) Final temperature of air,
`T_(f) = 1017.82^(0) C`

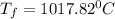
Step-by-step explanation:

The heat generated = Q

The work done = W

Time interval, Δt = 15 mins = 15 * 60

Δt = 900 s

It is stated that there is no overall change in kinetic and potential energy

`\triangle KE = 0\\\triangle PE = 0`

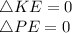
a) The change in internal energy, ΔU = Q - W

Change in specific internal energy, Δu = (Q - W)/m

Workdone is calculated by:

`W = \int {\dot{W}} \, dt \\W = \dot{W} \triangle t`

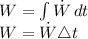
Since energy is transferred into the air, rate of energy transfer to the air is taken as negative,
`\dot{W} = -1 kW`

W = -1 * 900

W = - 900 kJ

Energy received by heat transfer,
`\dot{Q} = 0.5 kW`

`Q = \int {\dot{Q}} \, dt \\Q = \dot{Q} \triangle t`

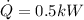
Q = 0.5 * 900

Q = 450 kJ

Mass of air, m = 2 kg

Change in specific internal energy, Δu = (Q - W)/m

Δu = (450 - (-900)/2

Δu = 675 kJ

b) By interpolation from the ideal gas property table:

At
`T_(i) = 200^(0) C = 473 K\\`

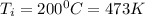
When T = 470K, u = 337.32 kJ/kg

When T = 480K, u = 344.70

`(u_(i) - 337.32 )/(344.7 - 337.32) = (473 - 470 )/(480 -470)`

`u_(i) = 339.534 kJ/kg`

`\triangle u = u_(f) - u_(i)\\675 + 339.534 = u_(f)\\u_(f) = 1014.534 kJ/kg`

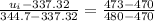
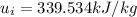
At
`u_(f) = 1014.534 kJ/kg`

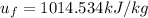
When T = 1280K, u = 1004.76 kJ/kg

When T = 1300K, u = 1022.82 kJ/kg

By interpolation,

`(T_(f) - 1280 )/(1300 - 1280) = (1014.534 - 1004.76 )/(1022.82 -1004.76)\\T_(f) = 1290.82 K// T_(f) = 1290.82 - 273 \\ T_(f) = 1017.82^(0) C`