Answer:
a) the temperature to which the pin must be cooled for assembly is
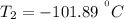
b) the radial pressure at room temperature after assembly is
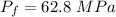
c) the safety factor in the resulting assembly = 6.4
Step-by-step explanation:
Coefficient of thermal expansion
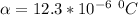
Yield strength
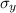 = 400 MPa
= 400 MPa
Modulus of elasticity (E) = 209 GPa
Room Temperature
 = 20°C
= 20°C
outer diameter of the collar
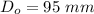
inner diameter of the collar

pin diameter
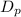 =
=
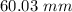
Clearance c = 0.06 mm
a)
The temperature to which the pin must be cooled for assembly can be calculated by using the formula:
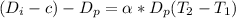
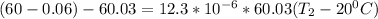
-0.09 =
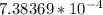
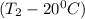
-0.09 =
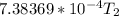
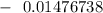
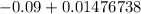 =
=
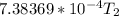
−0.07523262 =
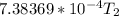
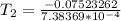
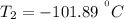
b)
To determine the radial pressure at room temperature after assembly ;we have:

c) the safety factor of the resulting assembly is calculated as:
safety factor =
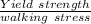
safety factor =
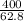
safety factor = 6.4
Thus, the safety factor in the resulting assembly = 6.4