Question

An automated transfer line is to be designed. Based on previous experience, the average downtime per occurrence = 5.0 min, and the probability of a station failure that leads to a downtime occurrence is 0.01. The total work content time = 39.2 min and is to be divided evenly among the workstations, so the ideal cycle time for each station = 39.2/n, where n is the number of workstations.

Determine; (a) the optimum number of stations on the line that will maximize production rate and b) the production rate Rp and proportion uptime for answer to part (a).

Answer 1

a) 28 stations

b) Rp = 21.43

E = 0.5

Step-by-step explanation:

Given:

Average downtime per occurrence = 5.0 min

Probability that leads to downtime, d= 0.01

Total work time, Tc = 39.2 min

a) For the optimum number of stations on the line that will maximize production rate.

Maximizing Rp =minimizing Tp

Tp = Tc + Ftd

`= (39.2)/(n) + (n * 0.01 * 5.0)`

`= (39.2)/(n) + (n * 0.05)`

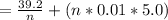
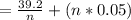
At minimum pt. = 0, we have:

dTp/dn = 0

`= (-39.2)/(n^2) + 0.05 = 0`

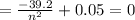
Solving for n²:

`n^2 = (39.2)/(0.05) = 784`

`n = √(784) = 28`

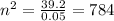
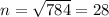
The optimum number of stations on the line that will maximize production rate is 28 stations.

b)
`Tp = (39.2)/(28) + (28 * 0.01 * 5)`

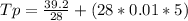
Tp = 1.4 +1.4 = 2.8

The production rate, Rp =

`(60min)/(2.8) = 21.43`

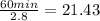
The proportion uptime,

`E = (1.4)/(2.8) = 0.5`