Answer:
x+ y = 0
and
-2x + 5y + 2 = 0
Explanation:
given line
3x+5y+2=0
5x+3y-2=0
solution
when two line bisect each other then line equation of bisector is express as
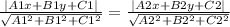 .........................1
.........................1
and here
A1 = 3
B1 = 5
C1 = 2
and
A2 = 5
B2 = 3
C2 = -2
so now put value in equation 1 we get
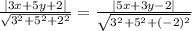
solve it we get
-2x + 5y + 2 = 0 ..........1
and
3x+5y+2 = - ( 5x+3y-2 )
solve it we get
8x + 8y = 0
x + y = 0 ................2