Question

find an equation of the line that bisects the acute angle formed by the graphs of 3x+5y+2=0 and 5x+3y-2=0

Answer 1

D. x+y=0

Explanation:

Edge 2021

Answer 2

x+ y = 0

and

-2x + 5y + 2 = 0

Explanation:

given line

3x+5y+2=0

5x+3y-2=0

solution

when two line bisect each other then line equation of bisector is express as

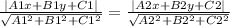`(|A1x+B1y+C1|)/(√(A1^2+B1^2+C1^2)) = (|A2x+B2y+C2|)/(√(A2^2+B2^2+C2^2))` .........................1

and here

A1 = 3

B1 = 5

C1 = 2

and

A2 = 5

B2 = 3

C2 = -2

so now put value in equation 1 we get

`(|3x+5y+2|)/(√(3^2+5^2+2^2)) = (|5x+3y-2|)/(√(3^2+5^2+(-2)^2))`

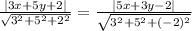
solve it we get

-2x + 5y + 2 = 0 ..........1

and

3x+5y+2 = - ( 5x+3y-2 )

solve it we get

8x + 8y = 0

x + y = 0 ................2