Answer:
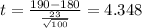
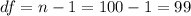
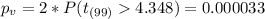
Since the p value obtained for this case is a very low value we have enough evidence to reject the null hypothesis that the true mean is equal to 180 at many of the possible significance levels commonly used. So then makes sense the claim that the true mean for the weigth is different from 180
Explanation:
Information provided
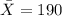 represent the mean weight
represent the mean weight
 represent the sample standard deviation for the weight
represent the sample standard deviation for the weight
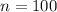 sample size
sample size
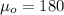 represent the value to compare
represent the value to compare
t would represent the statistic
 represent the p value
represent the p value
System of hypothesis
We want to determine if the true mean weight is different from 180 pounds, the system of hypothesis would be:
Null hypothesis:
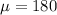
Alternative hypothesis:

We don't know the population deviation for the variable of interest so then the statistic is given by:
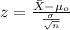 (1)
(1)
Replacing the data given we got:
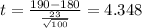
Now we can find the p value but first we need to find the degrees of freedom given by:
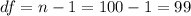
Since we are conducting a two tailed test the p value can be calculated on this way:
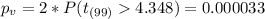
Since the p value obtained for this case is a very low value we have enough evidence to reject the null hypothesis that the true mean is equal to 180 at many of the possible significance levels commonly used. So then makes sense the claim that the true mean for the weigth is different from 180