Answer:
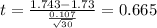
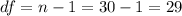
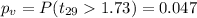
And if we compare the p value obtained and the significance level provided of 0.05 or 5% we see that
 so then we have enough evidence to conclude that the true mean for this case is significantly higher tha 1.73 since we reject the null hypothesis for the test
so then we have enough evidence to conclude that the true mean for this case is significantly higher tha 1.73 since we reject the null hypothesis for the test
Explanation:
We have the following dataset given:
1.7, 1.6, 1.8, 1.9, 1.75, 1.83, 1.82, 1.65, 1.95, 1.69, 1.82, 1.87, 1.65, 1.54, 1.98, 1.78, 1.69, 1.75, 1.62, 1.64, 1.75, 1.8, 1.65, 1.7, 1.82, 1.62, 1.83, 1.75, 1.7, 1.65
We can calculate the sample mean and deviation from this data with the following formulas:

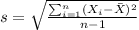
And replacing we got:
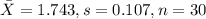
From previous info we know that 10 years before, the average height of persons in country A was determined to be 1.73 and standard deviation is 0.2.
We can use a one t test in order to check the claim that he average height of individuals in country A has increased in the last 10 years
Null hypothesis:
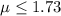
Alternative hypothesis:
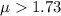
The statistic is given by:
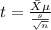
Replacing the info given we got:
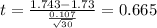
The degrees of freedom for this test are given by:
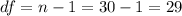
Now we can calculate the p value with the following probability:
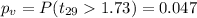
And if we compare the p value obtained and the significance level provided of 0.05 or 5% we see that
 so then we have enough evidence to conclude that the true mean for this case is significantly higher tha 1.73 since we reject the null hypothesis for the test
so then we have enough evidence to conclude that the true mean for this case is significantly higher tha 1.73 since we reject the null hypothesis for the test