Question

Quincy uses the quadratic formula to solve for the values of x in a quadratic equation. He finds the solution, in simplest radical form, to be x = StartFraction negative 3 plus or minus StartRoot negative 19 EndRoot Over 2 EndFraction.

Which best describes how many real number solutions the equation has?

Zero, because the discriminant is negative.
Zero, because the discriminant is not a perfect square.
One, because the negative and the minus cancel each other out.
Two, because of the ± symbol.

Answer 1

We have been given that Quincy uses the quadratic formula to solve for the values of x in a quadratic equation. He finds the solution, in simplest radical form, to be
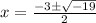`x=(-3\pm√(-19))/(2)`. We are asked to choose the correct option about real number of solutions.

We can see from Quincy's work that the value under radical is negative. That value is known as discriminant.

We know that quadratic formula is
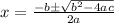`x=(-b\pm√(b^2-4ac))/(2a)`. The value
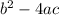`b^2-4ac` is known as discriminant.

`D=b^2-4ac`

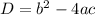
If
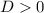`D>0`, then equation has two real solutions.

If
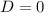`D=0`, then equation has one real solution.

If
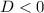`D<0`, then equation has no real solutions.

We can see from our given information that
`d=-19<0`.

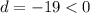Since discriminant is negative (less than 0), therefore, the equation will have no real solutions and 1st option is the correct choice.