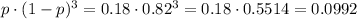Question

Data from the U.S. Bureau of Labor Statistics show a steady decline in the average workweek of U.S. production workers from 38.5 hours in 1964 to 33.9 hours in 2006. But employees are spending time working when they are at home and behind the wheel. In a poll conducted for Staples, 18% of small-business managers in the United States reported that they read e-mail messages in the bathroom. Consider the experiment of randomly selecting four small-business managers and learning whether they read e-mail messages in the bathroom.

Let R = reads e-mail in the bathroom, and
N = does not read e-mail in the bathroom.
Firs, define a success, in this case, define the selection of a manager who reads e-mail in the bathromm as success. Of the________possible experimental outcomes, _________outcomes result in exactly 1 success.
All of the sample points with 1 success have the same probability of occurrence. What is this probability?
a. 0.18
b. 0.0048
c. 0.0218
d. 0.0992

Answer 1

Of the 16 possible experimental outcomes, 4 outcomes result in exactly 1 success.

The probability of a determined sample point with an outcome of one success is P=0.0992.

Explanation:

We have a proportion of success (the selection of a manager who reads e-mail in the bathroom) of p=0.18.

The sample size is n=4.

We can model this as a binomial random variable.

The sample space is [0, 1, 2, 3, 4].

The possible outcomes for x=0 (that is no manager in the sample reads email in the bathroom) can be calculated as:

`C(0)=\dbinom{4}{0}=(4!)/(4!0!)=1`

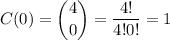
The same way we can calculate all the other possible outcomes:

`C(1)=\dbinom{4}{1}=(4!)/(3!1!)=(4)/(1)=4\\\\\\C(2)=\dbinom{4}{2}=(4!)/(2!2!)=(4*3)/(2*2)=6\\\\\\C(3)=\dbinom{4}{3}=(4!)/(3!1!)=4\\\\\\C(4)=\dbinom{4}{4}=(4!)/(4!0!)=1`

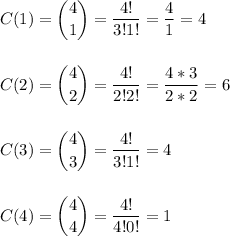
The sum of this outcomes is 16 possible outcomes. Of the 16 possible experimental outcomes, 4 outcomes result in exactly 1 success.

The probability of an outcome with 1 success is the product of p (the one that reads email) times (1-p)^3 (the other 3 that do not read emails in the bathroom):

`p\cdot (1-p)^3=0.18\cdot0.82^3=0.18\cdot 0.5514=0.0992`