Answer:
Examine each term of the polynomial to determine whether it is even, odd, or neither.
- Even = each term is an even function
- Odd = each term is an odd function
- Neither = terms are even and odd terms
Even function → symmetry about the y-axis
Odd function → symmetry about the origin
1) y = x⁴ is an even function, as it has symmetry about the y-axis
y = x² is an even function, as it has symmetry about the y-axis
Therefore, x⁴ + x² is an even polynomial
2)
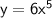 is an odd function, as it has symmetry about the origin.
is an odd function, as it has symmetry about the origin.
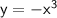 is an odd function, as it has symmetry about the origin.
is an odd function, as it has symmetry about the origin.
Therefore,
 is an odd polynomial
is an odd polynomial
**Please see attachments for examples of even and odd functions**