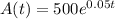Answer:
(C)
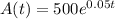
Explanation:
If A(t) represent the amount of money in a bank account at time t years.
The rate at which the account is increasing is proportional to the amount of money in the account, which is modeled by the differential equation:
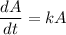
First, we solve this differential equation

At the moment when the amount of money in the account is $1000, the amount is increasing at a rate of $50 per year.
When A(t)=$1000,
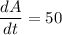
Therefore:
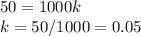
Substituting into our result from A(t) above: