Question

1. A drawing of a triangular park shows that the sides measure 12 m, 30 m, and 18 m. Can these dimensions be correct?

2. Find the measure of angle A.

Answer 1

Answer: 1. It is not possible to construct a triangle of given measure sides.

2. The value of ∠A is 44°

Explanation:

1.

Given: Three sides of a triangle

Let a= 12 m , b=30 m and c= 18 m

Now as we know

The sum of two sides of a triangle is always greater than the third side

Therefore we need to show

a+b>c -----(i)

b+c>a -----(ii)

c+a>b -----(iii)

(i a+b= 12+30 = 42>18= b ⇒ a+b>c

ii) b+c=30+18= 48 >12=a ⇒ b+c>a

iii) c+a=18+12=30=b ⇒ c+a= b

Therefore the third condition does not verified

Hence, it is not possible to construct a triangle of given measure sides.

2.

As we now triangle sum property which states that the sum of all the three angles of a triangle is 180°

So we have

`x+59+84+x+51=180\\\\\Rightarrow 194 +2x=180\\\\\Rightarrow 2x= 180-194\\\\\Rightarrow 2x=-14\\\\\Rightarrow x= -7`

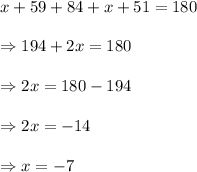
Therefore

`\angle A = x+51= -7+51= 44^\circ`

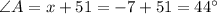
Hence, the value of ∠A is 44°