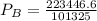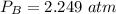Question

Water at a gauge pressure of 3.8 atm at street level flows into an office building at a speed of 0.78 m/s through a pipe 5.0 cm in diameter. The pipe tapers down to 2.8 cm in diameter by the top floor, 16 m above, where the faucet has been left open.

Calculate the flow velocity and the gauge pressure in the pipe on the top floor. Assume no branch pipes and ignore viscosity.

Answer 1

The flow velocity is
`v_A = 2.4869 \ m/s`

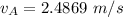
The gauge pressure is
`P_B = 2.249 \ atm`

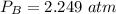
Step-by-step explanation:

The diagram for this question is shown on the first uploaded image

From the question we are told that

The gauge pressure
`P_A = 3.8 \ atm = 3.8 * 101325 = 385035 \ Pa`

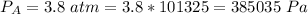
The speed of flow is
`v_A = 0.78 m/s`

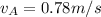
The diameter of the pipe is
`d = 5.0 cm = (5)/(100) = 0.05 \ m`

The diameter at the top floor is
`d_1 = (2.8)/(100) = 0.028 \ m`

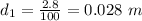
The the height from the ground is
`h_B = 16 m`

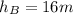
So we are going to make some assumption

We would assume that the position on the street is A

and the position on the top floor is B

So from continuity equation the velocity of the flow in the street is

`v_A = (V_B * a_B)/(a_A)`

Where

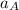`a_A` is the area of the pipe at the base

So

`a_A = (\pi d^2)/(4)`

`a_A = ( 3.142 * (5)^2)/(4)`

`a_A =19.64 m^2`

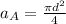
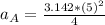
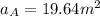
and
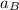`a_B` i the area of the pipe at the top floor

`a_B = (\pi d^2)/(4)`

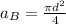
substituting values

`a_B = ( 3.142 * (2.8) )/(4)`

`a_B = 6.16 \ m^2`

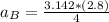
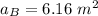
So

`v_A = (0.78 * 19.64 )/(6.16)`

`v_A = (0.78 * 19.64 )/(6.16)`

`v_A = 2.4869 \ m/s`

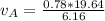
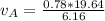
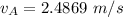
Applying Bernoulli's equation

`P_A + \rho g h_A + (1)/(2) \rho v_A ^2 = P_2 + \rho g h_B + (1)/(2) \rho v_B^2`

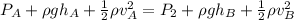
Since the pipe started from the floor
`h_A = 0m`

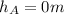
Here the
`\rho` is the density of water with value
`\rho = 1000 \ kg/m^3`

Substituting values

`385035 + (1000* 9.8 * 0 ) + (1)/(2) * 1000 * 0.78^2 = \\`

`P_B + 1000 * 9.81 *16 + (1)/(2) * 1000 * 2.487^2`

`P_B = 225446.6 \ Pa`

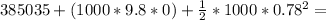
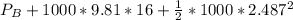
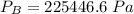
Converting back to atm

`P_B = (223446.6)/(101325)`

`P_B = 2.249 \ atm`

Answer 2

`v_2` = 2.49 m/s

`P_2` = 2.19 atm

Step-by-step explanation:

By using continuity equation:

`v_2` = (
`A_1`
`v_1`) /
`A_2` = (
`d_1 / d_2`)²
`v_1` = (5/2.8)² x 0.78 = 2.49 m/s

By using Bernoulli’s Equation:

`P_1` + ρg
`h_1` + ½ρ (
`v_1` )²=
`P_2` + ρg
`h_2` + ½ρ(
`v_2` )²

[
`v_1` ² -
`v_2` ²] /2 = (
`P_2`-
`P_1` )/ ρ + g(
`h_2` -
`h_1`)

(0.78²- 2.49²)/2 = (
`P_2`-
`P_1` )/ 1000 + (9.8 x 16)

-5.6= (
`P_2`-
`P_1` )/ 1000 + (156.8)

(
`P_2`-
`P_1` ) = - 162400 Pa

`P_2` =
`P_1` -162400,
`P_1` = 3.8atm = 385035 Pa

`P_2` = 385035-162400 = 222635 Pa ( gauge pressure)

`P_2` = 222635 Pa=> 2.19 atm