Answer:
Therefore orthocentre is ( 5 , 1.5 )
Explanation:
From the general equation of a circle,
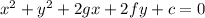
Substitute K(2, -2), L(4,6), M(8,-2) in (x,y)
K(2, -2): 2^2 +(-2)^2 + 2g(2) + 2f(-2) + c = 0
4g - 4f + c = -8
Divide by 4: g - f + c = -2 -----------(1)
L(4,6): 4^2 + 6^2 + 2g(4) + 2f(6) + c = 0
8g + 12f + c = -52
Divide by 4: 2g + 3f + c = -13 ----------(2)
M(8,-2): 8^2 +(-2)^2 + 2g(8) + 2f(-2) + c = 0
16g - 4f + c = -68
Divide by 4: 4g - f + c = -17 ----------(3)
Equation (2) - (1)
g + 4f = -11
g = -11 - 4f -----------(a)
Equation (3) - (2)
2g - 4f = -4
2g = -4 + 4f ----------(b)
Substitute for g in eqn (b)
2(-11 - 4f) = -4 + 4f
-12f = 18
f = -1.5
From eqn (a)
g = -11 - 4(-1.5)
g = -5
Since the orthocentre is given by (-g,-f)
Therefore orthocentre is (5,1.5)