Question

A 1.10 m wire has a mass of 5.90 g and is under a tension of 160 N. The wire is held rigidly at both ends and set into oscillation. (a) What is the speed of waves on the wire? What is the wavelength of the waves that produce (b) one-loop and (c) two-loop standing waves? What is the frequency of the waves that produce (d) one-loop and (e) two-loop standing waves?

Answer 1

a) 172.77 m/s

b) 2.2 m

c) 1.1 m

d) 78.53 Hz

e) 157.06 Hz

Step-by-step explanation:

Given that

Length of wire, l = 1.1 m

Mass of wire, m = 5.9 g = 0.0059 kg

Tension of the wire, T = 160 N

a)

v = √(T / μ), where μ = l/m, thus

v = √(T /(m/l))

v = √(160 /(0.0059/1.1))

v = √(160 / 0.00536)

v = √29851

v = 172.77 m/s

b)

λ(1) = 2l / n

λ(1) = (2 * 1.1) / 1

λ(1) = 2.2 m

c)

λ(2) = 2l / n

λ(2) = (2 * 1.1) / 2

λ(2) = 1.1 m

d)

f(1) = n * v/2l

f(2) = 172.77 / (2 * 1.1)

f(2) = 78.53 Hz

e)

f(2) = n * v/2l

f(2) = 2 * 172.77/(2 * 1.1)

f(2) = 157.06 Hz

Answer 2

a)v= 172.7m/s

b)λ
`Ф_(1)` =2.2m

c)λ
`Ф_(2)` = 1.1m

d)f= 78.5 Hz

e)f= 157 Hz

Step-by-step explanation:

Length 'L'=1.1 m

mass 'm'= 5.9g =>0.0059kg

Tension 'T'= 160N

a)the speed of a wave on strecteed string is given by,

v= √T/μ

where μ is mass per unit length

v=
`\sqrt{(T)/(m/L) }` =>
`\sqrt{(160)/((0.0059)/1.1) }`

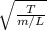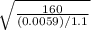
v= 172.7m/s

b)The general formula for the wavelength of the waves that produce one-loop is guven by,

λ = 2L/n

λ
`Ф_(1)` = 2(1.1)/1 =>2.2m

c)the wavelength of the waves that produce two-loop is given by,

λ
`Ф_(2)` = 2(1.1)/2 =>1.1m

d) For the frequency of the waves that produce one-loop waves:

f= n
`(v)/(2L)` (n=1)

f=
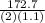`(172.7)/((2)(1.1))` => 78.5 Hz

e)For the frequency of the waves that produce two-loop standing waves:

f= n
`(v)/(2L)` (n=2)

f= 2 x
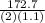`(172.7)/((2)(1.1))` => 157 Hz